2022/05/22
【最適化】グループ分けを最適化する!②遺伝的アルゴリズムという最適化手法

このシリーズでは全4回にわたって,最適化手法を用いた研究室でのゼミグループ分けプログラム作成の軌跡をたどります.最適化問題を基礎から応用まで実例ベースで扱うので,初学者から実践的な利用事例を求める専門家まで,様々な方に読んでいただけます.
今回は第2回ですので,前回の記事をまだ読んでいない方はぜひ読んでみてください!https://www.ds.se.shibaura-it.ac.jp/?p=2229
第2回では,今回利用する最適化手法の紹介を行います.最適化手法には,遺伝子を模した遺伝的アルゴリズム(以下,GA)や,金属工学に由来する焼きなまし法(SAと略される)などがあります.市川研究室のグループ分けでは,多くの論文で離散的最適化に優れていると述べられていることから,GAを用いて実装することに決定しました.様々な最適化手法の一般論は,すでに別の方々が詳しく述べられていますので,ここでは市川研究室のグループ分けに沿って,活用方法のひとつとしてまとめていきます.
最適化手法,遺伝的アルゴリズム
まず,GAの基本についておさらいしましょう.GAとは,遺伝子(解)を複数持つ初期集団に対して,適応度の評価→選択(淘汰)→交叉→突然変異→適応度の評価→…と行程を繰り返し,最終的に残った集団の最高の遺伝子を最適解とする方法です.(右画像は自分のノートです.白字がGAのフロー,緑字は各工程における種々の方法,その他メモですのでお見捨ておきください…)
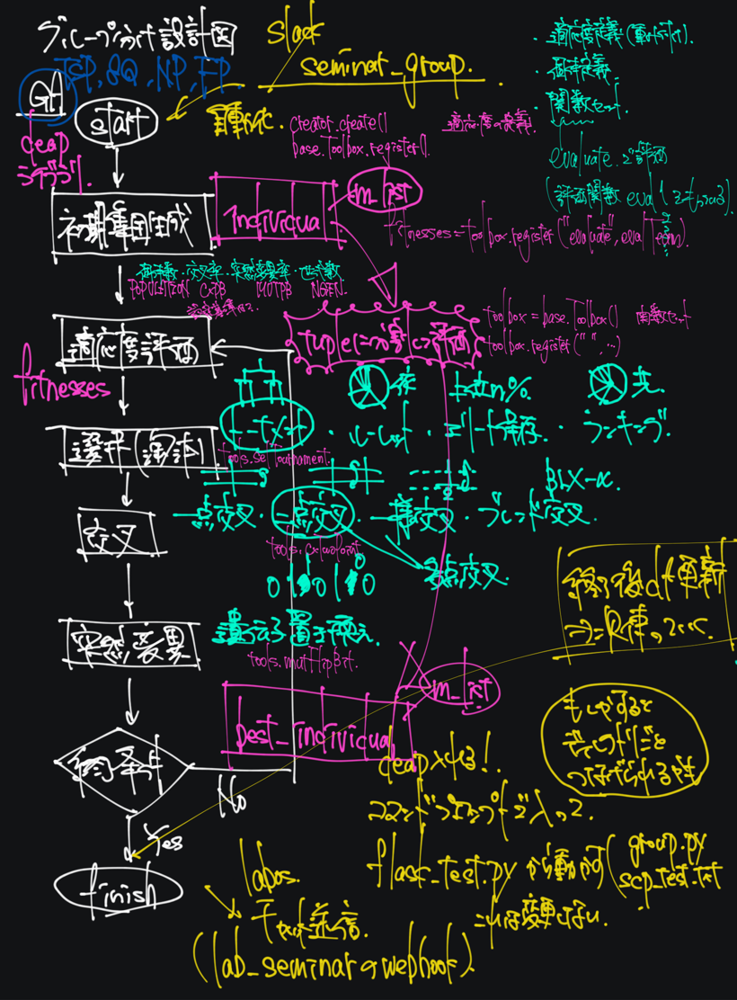
各行程には,種々の方法が用意されています.今回は選択(淘汰)にトーナメント方式を,交叉に二点交叉を採用しました.また評価には,学年・リーダー/グループ1になった回数(注1)・個人間で同じグループになった回数を用いて,前回まとめた制約条件に照らしてよりよい集団(遺伝子)に替えていきます.
注1:「リーダー/グループ1になった回数」について,リーダーは朝礼と終礼を行うグループ(いわゆる週報グループ)の役割,グループ1はゼミグループ(新聞記事ゼミなどを行なっています,これについてはまた別の記事で!)のことなので,別に集計するようプログラムしていきます.
制約条件に対する定式化
さて,評価について詳しくみていきましょう.
1.学年について
市川研究室は,比較的修士課程の学生が多いことが強みのひとつです.グループの中に各学年が1人以上いる状態をつくり,終礼などのタイミングで,経験値がある学生がグループ内のメンバーにそれなりのアドバイスを行うことで,研究室全体のレベルが上がっていきます.
個人の学年属性を用いて,「各学年が1人以上」含まれるように計算していきます.将来的には「各学年レベルが1人以上」,つまり学部生であっても修士生レベルであればその属性を付与し,参照することで動的なグループ分けを行うことを目指します.
2.リーダー/グループ1になった回数・個人間で同じグループになった回数について
前回記事でも触れたとおり,全員に均等に役割や先生からのコメントの機会を振り,様々なメンバーとグループを共にすることが重要です.特に最近では,誰が何をどのように研究しているのかを知ることの重要性が研究室内で再確認されています.
全体の最大最小差が小さくなるように計算していきます.例えばリーダーを一番やったことのある人が4回で,一番やったことのない人が2回であれば,全体の中からリーダーをやった回数が2回または3回のメンバーを各チームに配置することで最大最小差を小さく(それ以下に)します.
まとめ
いかがだったでしょうか.今回は研究室のグループ分けについて,GAを利用していくことが決まり,の制約条件に対する評価方法も決定しました.次回は,これを実際にプログラミングしてグループ分けします.そちらもご覧ください!
著者プロフィール





