2022/05/11

【最適化】グループ分けを最適化する！①制約条件の整理

このシリーズでは全4回にわたって、最適化手法を用いた研究室でのゼミグループ分けプログラム作成の軌跡をたどります。最適化問題を基礎から応用まで実例ベースで扱うので、初学者から実践的な利用事例を求める専門家まで、様々な方に読んでいただけます。

まず第1回(今回)では、最適化問題の定義を紹介し、実際のグループ分けにおける制約条件を整理します。第2回で最適化手法の紹介を行い、第3回で実際にプログラムを実行し、第4回でSlackでの結果送信を自動化するところまでそれぞれ解説します。

グループ分けという最適化問題

一般に、最適化問題とは、与えられた制約条件の下で目的関数の値を最小（もしくは最大）にする解を求める問題です。例えば、セールスマンがn個の都市を1度ずつ訪問し出発点に戻るときの、総移動距離を最小にする巡回路を求める問題(巡回セールスマン問題)は有名です。以下は巡回セールスマン問題の総当たり解法イメージです。

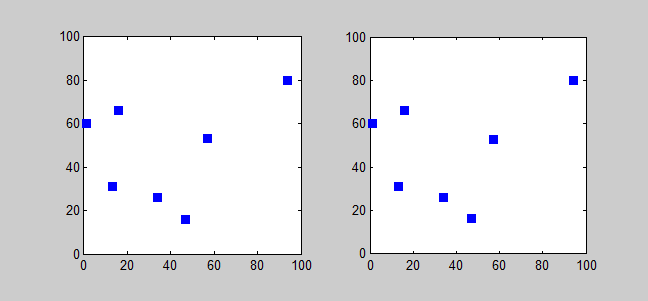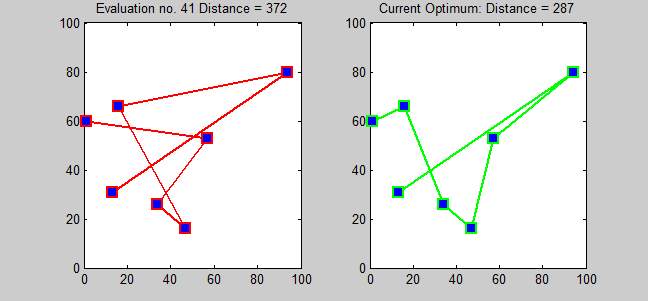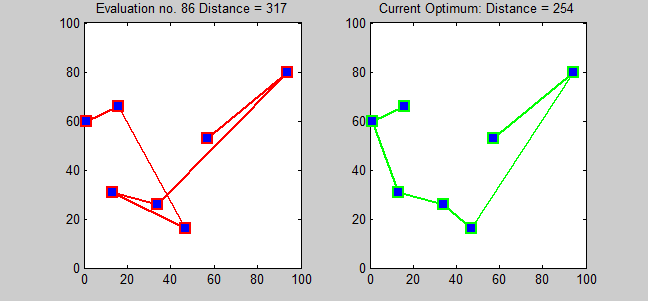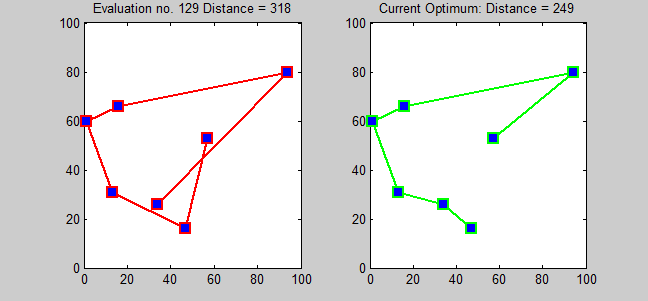
https://commons.wikimedia.org/w/index.php?curid=23385682による

市川研究室では、26名のメンバーが5つのグループに分かれて、毎週月曜日に朝礼・毎週金曜日に終礼というものを行っています。朝礼ではその1週間でどのようなタスクをこなすのか共有し、終礼ではその1週間でどのような進捗があったのか共有します。そのほかにもゼミなどでグループ分けの機会があります。

ここで、高質な研究室活動に貢献するための仕組みのひとつとして、メンバー全員が高めあえるグループ分けを実施するわけです。つまりグループ分けを最適化問題ととらえ、これに対応する最適なグループ解を出すのです。今回は、このときの制約条件を整理していきます。

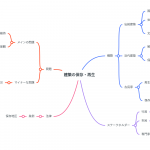
制約条件の整理

まずは、グループ分けに必須の条件を整理していきます。

1人を1チームに割り当てる
各チームの人数を均一にする

「当たり前じゃないか」と思われるかもしれませんが、これも大事な条件です。グループを掛け持ちすることや、チームの人数にばらつきが出ることを防がなくてはなりません。

さらに、よりよいグループ分けに向けて条件を追加していきます。

各チームでメンバーのグループ1になった回数の合計を平坦にする
各チームでメンバーのリーダーになった回数の合計を平坦にする
各チームに各学年1名以上割り当てる
個人間で同じグループになった回数を平均化する

今度は「グループ1になった回数が同じになってどうするんだ」と感じてもらえたでしょうか。ゼミでは、市川先生がグループ1を中心にコメントをしてくださるので、平等にグループ1に振り分けられる必要があるのです。リーダーもみなが平等に経験し、チーム内では学年が混在し、いつもとは違う人と意見を交わしあうこともまた重要です。